Likelihood Models
Jed Rembold
April 16, 2024
Announcements
- Only 1 more homework assignment!
- The last homework assignment (HW5) will thus be due April 26
- Quiz 2 handed back!
- HW2 feedback continues
- Poll will be going out about partner preferences on final group
project
- Please respond promptly, as I want to get groups made by Thursday
Recap
- A Monte Carlo Markov Chain is a semi-random walk wherein the next step is determined by the current location and a bit of randomness
- Directed in the sense that is has a preference to move “uphill”, toward higher parts of the function it is sampling
- By letting the sampling run for a while, and keeping track of where
the walker has been, you can regenerate the walked function by looking
at a histogram of where the walker spent the most time
- Really just regenerate the shape, the scaling will be different
Today
- How does this all apply to fitting models?
- Baye’s Theorem
- Priors and Likelihood
- Walking the probability
- Analysis
Model Fitting and Baye’s Theorem
- Here we are not as concerned with the best fit
- Concerned instead with our confidence about our fit parameters
- “What was the probability of getting these parameters given this data?”
- Baye’s Theorem provides a way to compute this probability \[ P(\theta | D) = \frac{P(D | \theta) \cdot P(\theta)}{P(D)} \] where \(\theta\) represents our fit parameters and \(D\) represents the data
- For our purposes, viewing this through a Bayesian lens will be more informative
Baye Life
The Breakdown (Part I)
- The Prior is the probability of the parameters
without any consideration of the data
- This generally reflects any knowns or assumptions you are making about the parameters
- Are they all positive? Are they bounded in some way?
- The Likelihood is the probability of getting the
data given the parameters
- For model fitting, this is where we compare the actual data to the predicted data by our model
- The better the match, the greater the likelihood
The Breakdown (Part II)
- The Evidence is the probability of the data being
the way it is
- This is extremely hard to measure, and also largely pointless for our use-case
- It doesn’t depend on the parameters, so would just be a constant scaling factor
- The Posterior is the probability of the parameters
given the data
- This is what we want!
- “How likely are these parameters given our data?”
The Big Picture
- Our goal here is to sample the right-hand side of Baye’s theorem using MCMC
- The resulting distribution would also describe the probabilities on
the left-hand side
- At least within a scaling factor
- What we are really interested in though is the spread of the posterior probability distribution, so this scaling is of no consequence to us
Logging
- We can get a pretty huge dynamic range when computing the values of the right-hand side
- Recall that we compute these for each step to see if we take the random step or not
- To avoid computational overflow/underflow errors, it can be recommended to work in ln-space instead
- Here, the accept/rejection step becomes: \[\frac{f(\theta^\prime)}{f(\theta)} > r \quad\rightarrow\quad \ln f(\theta^\prime) - \ln f(\theta) > \ln r \]
The Prior
Defining the prior pdf is usually straightforward
If using an unbounded, flat, prior, then it should just return 1 always (0 in ln-space)
If bounded, check the parameters and return 1 (0 in ln-space) if within the bounds or \(-\infty\) otherwise (
-np.infin Python,-Infin R)Pseudo-example:
|||function ln_prior(|||params|||)||| if |||illegal condition||| return -|||infinity||| return 0
The Likelihood
- The likelihood essentially compares the data our model would output to our actual data
- The goal is to minimize the differences between the two
- Additionally, things are normally scaled by known errors, so that values with more error have less weight
- As such: \[ P(\theta | D) \propto \exp(-\chi^2(\theta) / 2) \] where \[ \chi^2(\theta) = \sum_{i=1}^N \frac{(y_{i,D} - y_{i,\theta})^2}{\sigma_{i,D}^2} \]
The Likelihood (In Code)
The ln-likelihood then could look like:
|||function ln_likelihood(|||params, data|||)||| m,b = params x,y,errY = data # extract data y_model = m * x + b # compute model result return - 0.5 * |||sum(||| (y - y_model) ** 2 / errY ** 2 |||)|||
All together now…
Bring both pieces together (since we don’t care about \(P(D)\)):
|||function ln_pdf(|||params, data|||)||| p = |||call ln_prior||| if p == -|||infinity||| # no sense continuing return -|||infinity||| return p + ln_likelihood(params, data)
Extended Example
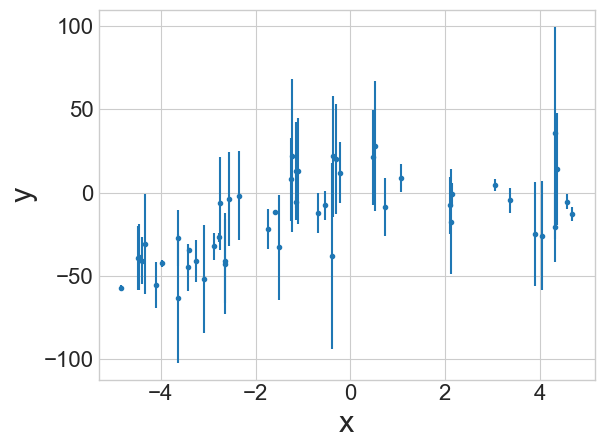
Suppose we want to evaluate the uncertainties in our parameters for a fit to the data to the right.
Our model will look something like: \[y = ax^2 + bx\]
MCMC does not tell you about the quality of a fit. It tells you about the variability in the fit parameters.
Burnin’
- If you have not started your parameter chain near the max, it takes a bit of time for the chain to find its way to the most probably area and start bouncing around
- We don’t care about this initial time period!
- Commonly called burn-in, and we throw away a certain number
of iterations before we start keeping track.
- This generally requires you to look at your parameters vs interations to decide when things reasonably leveled off.
Visualizing the Best Fit with Errors
- There are a few ways you can visualize the best fit model with uncertainties in the parameters reflected
- My go-to looks like:
- Randomly select some number of indices from your leveled chain
- For each index, grab the corresponding parameters and compute your model output with those parameters, appending the result to a list
- Compute the median and standard deviation of the results in your
list, being sure to specify
axis=0 - Plot the median values for your best approximation, and shade the region between the median - std and the median + std
Homework 5 Pairings!
- Last homework pairings!
- Left side:
- Dash and Siera
- Indi and Leila
- Trajan and Kara
- Michael and Alex
- Zachary and Owyn
- Right side:
- Sam and Matthew
- Nathaniel and Nico
- Teddy and Brandon
- Mia and Ben
- Paul and Sophia
- Kendall, Teo, and Jennifer